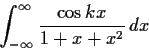Previous: Spring97
Next: Spring98
Preliminary Exam - Fall 1997
Problem 1
Define a sequence of real numbers
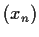
by
Show that
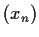
converges, and evaluate its limit.
Problem 2
Let
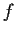
be a real valued function that is differentiable
on an open interval containing
![$[a, b]$](img5-49.gif)
.
Prove that if
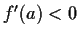
and
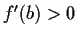
then there is
a point
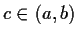
such that
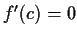
.
Problem 3
Let
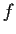
be an entire function such that, for all
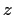
,
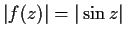
. Prove that there is a constant
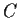
of modulus
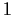
such that
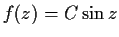
.
Problem 4
Evaluate the integral
where
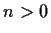
is an integer.
Problem 5
Let
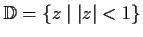
, the open unit disc in the complex plane.
Suppose that
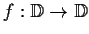
is analytic,
and that there exist two distinct points
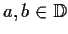
with
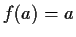
,
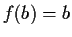
. Prove that
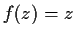
for all
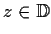
.
Problem 6
Let
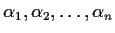
be distinct real numbers.
Show that the
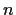
exponential functions
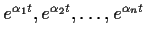
are linearly independent over the real numbers.
Problem 7
Define the
index of a real symmetric matrix
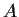
_matrix,>index
to be the number of strictly positive eigenvalues of
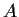
minus the number of strictly negative eigenvalues.
Suppose
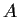
, and
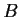
are real symmetric
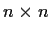
matrices
such that
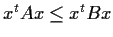
for all
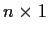
matrices
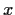
.
Prove the the index of
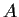
is less than or equal to the index of
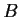
.
Problem 8
Suppose
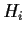
is a normal subgroup of a group
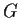
for
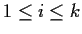
, such that
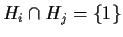
for
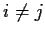
.
Prove that
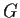
contains a subgroup isomorphic to
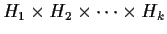
if
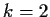
,
but not necessarily if
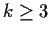
.
Problem 9
Prove that if
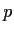
is prime then every group of order
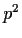
is abelian.
Problem 10
Prove that for all
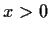
,
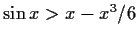
.
Problem 11
Let
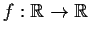
be twice differentiable,
and suppose that for all
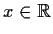
,
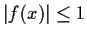
and
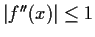
.
Prove that
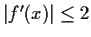
for all
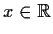
.
Problem 12
A map
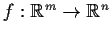
_map>compact _map>closed
is
proper if it is continuous and
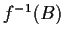
is compact for each compact subset
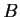
of
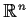
;
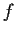
is
closed if it is continuous and
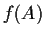
is closed
for each closed subset
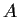
of
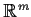
.
- Prove that every proper map
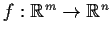 is closed.
is closed.
- Prove that every one-to-one closed map
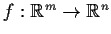 is proper.
is proper.
Problem 13
Conformally map the region inside the disc
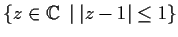
and outside the
disc
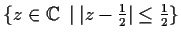
onto the upper half-plane.
Problem 14
Evaluate the integral
where
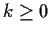
.
Problem 15
Let
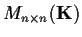
be the vector space of
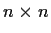
matrices over a field
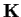
.
Find the dimension of the subspace of
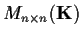
spanned by
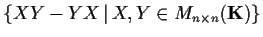
.
Problem 16
Prove that if
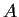
is a 2
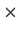
2 matrix over the integers
such that
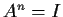
for some strictly positive integer
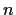
,
then
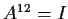
.
Problem 17
A group
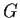
is generated by two elements
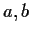
, each of order
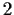
.
Prove that
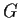
has a cyclic subgroup of index
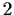
.
Problem 18
A finite abelian group
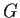
has the property that
for each positive integer
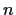
the set
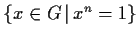
has at most
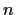
elements.
Prove that
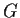
is cyclic,
and deduce that every finite field has cyclic multiplicative group.



Previous: Spring97
Next: Spring98
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10