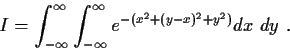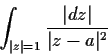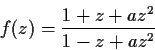Previous: Fall97
Next: Fall98
Preliminary Exam - Spring 1998
Problem 1
Prove that the polynomial
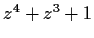
has exactly one root
in the quadrant
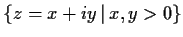
.
Problem 2
Let
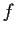
be analytic in an open set containing the closed unit disc.
Suppose that
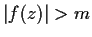
for
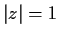
and
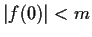
.
Prove that
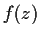
has at least one zero in the open unit disc
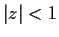
.
Problem 3
Let
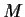
be a non-empty complete metric space. Let
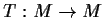
such that
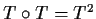
is a strict contraction. Prove that
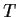
has a unique fixed point in
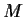
, i.e., there is a unique
point
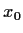
with
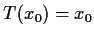
.
Problem 4
Using the properties of the Riemann integral, show that if
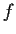
is a non-negative continuous function on
![$[0,1]$](img17-50.gif)
, and
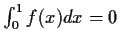
, then
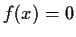
for all
![$x\in [0,1]$](img20-50.gif)
.
Problem 5
Let
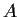
be the ring of real 2
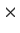
2 matrices of the form
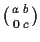
.
What are the 2-sided ideals in
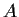
? Justify your answer.
Problem 6
Let
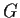
be the group
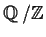
. Show that for every positive
integer
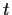
,
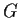
has a unique cyclic subgroup of order
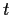
.
Problem 7
Suppose that
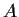
and
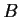
are two commuting
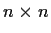
complex
matrices. Show that they have a common eigenvector.
Problem 8
Let
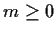
be an integer. Let
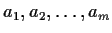
be integers and let
Show that if
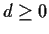
is an integer then
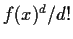
can be expressed in the form
where the
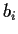
are integers.
Problem 9
Let
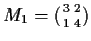
,
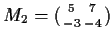
,
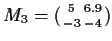
.
For which (if any)
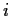
,
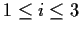
, is the sequence
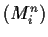
bounded away from
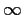
?
For which
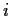
is the sequence bounded away from
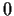
?
Problem 10
Let
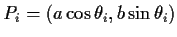
,
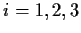
, be a triple
of points on the ellipse
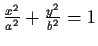
.
What is the maximal value of the area of the triangle
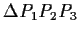
? Determine those triangles with maximal area.
Problem 11
Let
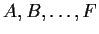
be real coefficients. Show that the
quadratic form
is positive definite if and only if
Problem 12
Given the fact that
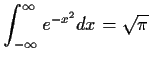
,
evaluate the integral
Problem 13
Let
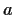
be a complex number with
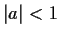
.
Evaluate the integral
Problem 14
Let
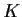
be a real constant. Suppose that
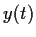
is a positive
differentiable function satisfying
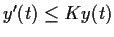
for
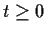
. Prove that
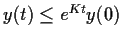
for
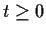
.
Problem 15
For continuous real valued functions
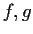
on the interval
![$[-1,1]$](img68-50.gif)
define the inner product
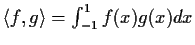
.
Find that polynomial of the form
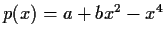
which is orthogonal on
![$[-1,1]$](img71-50.gif)
to all lower order polynomials.
Problem 16
Let
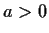
. Show that the complex function
satisfies
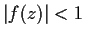
for all
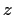
in the open left half-plane
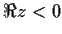
.
Problem 17
Let
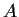
be an
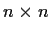
complex matrix with
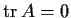
.
Show that
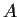
is similar to a matrix with all
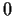
's along the main diagonal.
Problem 18
Let
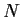
be a nilpotent complex matrix. Let
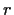
be a positive
integer. Show that there is a
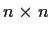
complex matrix
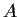
with



Previous: Fall97
Next: Fall98
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



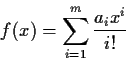
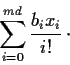
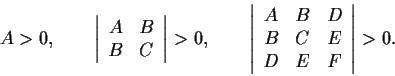
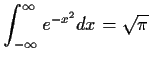 ,
evaluate the integral
,
evaluate the integral