Previous: Spring98
Next: Spring99
Preliminary Exam - Fall 1998
Problem 1
Let
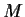
be a metric space with metric
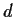
.
Let
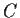
be a compact subset of

,
and let
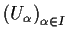
be an open cover of
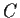
.
Show that there exists
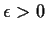
such that,
for every
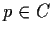
,
the open ball
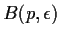
is contained in
at least one of the sets
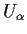
.
Problem 2
Find a function
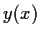
such that
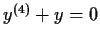
for
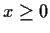
,
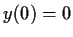
,

and
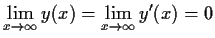
.
Problem 3
Prove that for any real

,
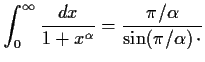
Problem 4
Let
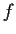
be analytic in the closed unit disc, with
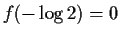
and
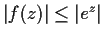
for all
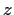
with
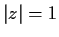
. How large can
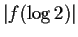
be?
Problem 5
Let

be a function such that
- the function
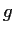 defined by
defined by
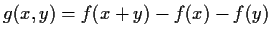 is bilinear,
is bilinear,
- for all
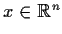 and
and
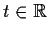 ,
,
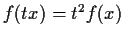 .
.
Show that there is a linear transformation

such that
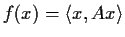
where
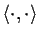
is the usual inner product on

(in other words,
is a quadratic form).
Problem 6
Let
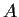
and
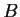
be linear transformations
on a finite dimensional vector space
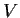
.
Prove that
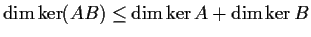
.
Problem 7
A real symmetric
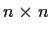
matrix
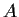
is called
positive semi-definite if
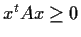
for all
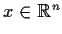
.
Prove that
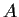
is positive semi-definite if and only if
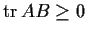
for every real symmetric positive semi-definite n
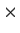
n matrix
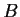
.
Problem 8
Let
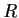
be a finite ring with identity.
Let
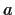
be an element of
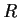
which is not a zero divisor.
Show that
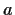
is invertible.
Problem 9
Suppose that
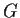
is a finite group such that
every Sylow subgroup is normal and abelian.
Show that
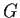
is abelian.
Problem 10
Let
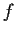
be a real function on
![$[a, b]$](img55-52.gif)
.
Assume that

is differentiable and that
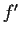
is Riemann integrable.
Prove that
Problem 11
Find the minimal value of the areas of hexagons circumscribing
the unit circle in
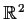
.
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 12
Let

be a function with
continuous second order partial derivatives such that
-
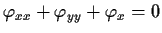 in the punctured plane
in the punctured plane
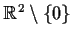 ,
,
-
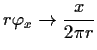 and
and
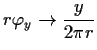 as
as
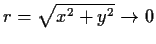 .
.
Let
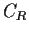
be the circle
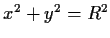
.
Show that the line integral
is independent of
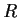
, and evaluate it.
Problem 13
Let

be an entire function.
Define
![% latex2html id marker 914
$\Omega = \mathbb{C}\setminus (-\infty, 0]$](img71-52.gif)
,
the complex plane with the ray
![$(-\infty, 0]$](img72-52.gif)
removed.
Suppose that for all

,
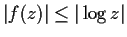
,
where
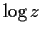
is the principal branch of the logarithm.
What can you conclude about the function

?
Problem 14
Let
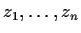
be distinct complex numbers, and let
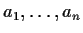
be nonzero complex numbers such that
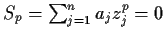
for
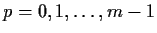
but
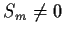
.
Here
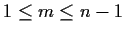
.
How many zeros does the rational function
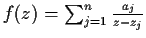
have in
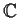
?
Explain why
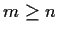
is impossible.
Problem 15
Let
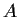
and
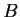
be n
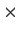
n matrices.
Show that the eigenvalues of
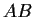
are
the same as the eigenvalues of
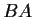
.
Problem 17
Let
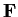
be a finite field with
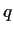
elements.
Denote by
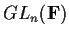
the group of
invertible n

n matrices with entries if
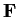
.
What is the order of this group?
Problem 18
Show that the field
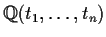
of rational functions in
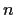
variables
over the rational numbers is isomorphic to a subfield of
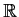
.



Previous: Spring98
Next: Spring99
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



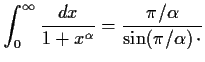
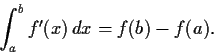
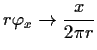 and
and
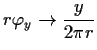 as
as