


Previous: Fall98
Next: Fall99
Preliminary Exam - Spring 1999
Problem 2
Suppose that a sequence of functions
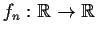
converges
uniformly on
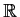
to a function
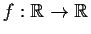
, and that
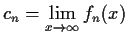
exists for each positive integer
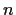
.
Prove that
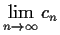
and
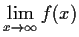
both exist and are equal.
Problem 3
Suppose that
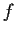
is a twice differentiable real-valued function on
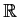
such that

,
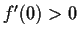
, and
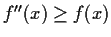
for all
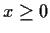
.
Prove that
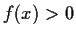
for all
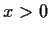
.
Problem 4
Evaluate
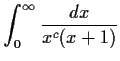
for each real number
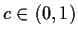
.
Problem 6
Let
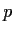
,
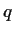
,
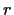
and
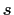
be polynomials of degree at most 3.
Which, if any, of the following two conditions is sufficient
for the conclusion that the polynomials are linearly dependent?
- At 1 each of the polynomials has the value 0.
- At 0 each of the polynomials has the value 1.
Problem 7
Suppose that the minimal polynomial of a linear operator
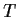
on a
seven-dimensional vector space is
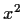
. What are the possible
values of the dimension of the kernel of T?
Problem 8
Let
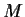
be a
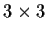
matrix
with entries in the polynomial ring
![% latex2html id marker 890
$\mbox{$\mathbb{R}^{}$}[t]$](img51-53.gif)
such that
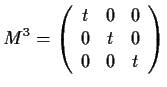
.
Let
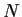
be the matrix with real entries
obtained by substituting
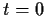
in
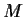
.
Prove that
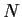
is similar to
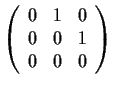
.
Problem 9
Let
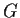
be a finite group, with identity
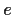
.
Suppose that for every
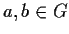
distinct from
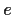
,
there is an automorphism
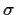
of
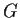
such that
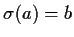
. Prove that
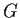
is abelian.
Problem 10
Suppose that
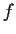
is a twice differentiable real function
such that
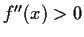
for all
![$x \in [a, b]$](img68-53.gif)
.
Find all numbers
![$c \in [a, b]$](img69-53.gif)
at which the area between the graph
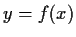
,
the tangent to the graph at
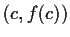
,
and the lines

,
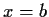
, attains its minimum value.
Problem 11
Prove that if
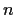
is a positive integer and
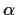
,
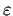
are real numbers with
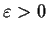
,
then there is a real function
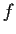
with derivatives of all orders such that
-
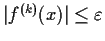 for
for
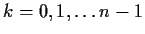 and all
and all
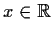 ,
,
-
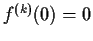 for
for
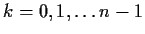 ,
,
-
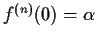 .
.
Problem 12
Suppose that
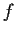
is holomorphic
in some neighborhood of
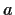
in the complex plane.
Prove that either
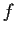
is constant on some neighborhood of
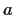
,
or there exist an integer
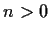
and
real numbers

such that
for each complex number
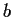
satisfying
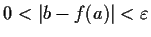
,
the equation
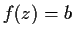
has exactly
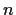
roots
in
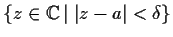
.
Problem 13
Let

,
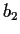
, ...be a sequence of real numbers such that

for all
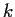
and
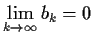
.
Prove that the power series
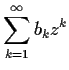
converges for all
complex numbers
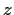
such that
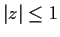
and
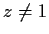
.
Problem 14
Let
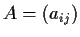
be a
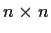
complex matrix
such that

if
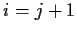
but
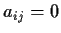
if
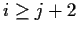
.
Prove that
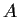
cannot have more than one Jordan block for any eigenvalue.
Problem 15
Let

be a square complex matrix,
and let
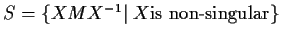
be the set of all matrices similar to
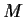
.
Show that
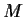
is a nonzero multiple of the identity matrix
if and only if no matrix in
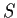
has a zero anywhere on its diagonal.
Problem 17
Let
![% latex2html id marker 1172
$f(x) \in \mbox{$\mathbb{Q}\,^{}$}[x]$](img130-10.gif)
be an irreducible polynomial of degree
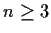
.
Let
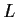
be the splitting field of
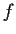
,
and let
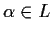
be a zero of
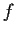
.
Given that
![% latex2html id marker 1186
$[L : \mbox{$\mathbb{Q}\,^{}$}] = n!$](img136-8.gif)
,
prove that
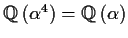
.
Problem 18
Let
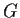
be a finite simple group of order
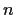
.
Determine the number of normal subgroups
in the direct product
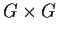
.



Previous: Fall98
Next: Fall99
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
 and
and  are closed in
are closed in  then
then 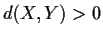 .
.
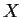 and
and  are compact then
are compact then  .
.
 is closed and
is closed and 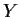 compact then
compact then 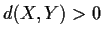 .
.



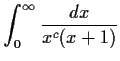 for each real number
for each real number 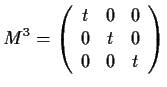 .
Let
.
Let 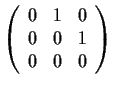 .
.
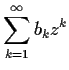 converges for all
complex numbers
converges for all
complex numbers 

