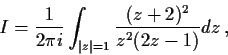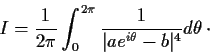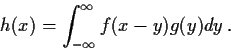Previous: Spring99
Next: Spring00
Preliminary Exam - Fall 1999
Problem 1
Let
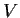
and
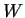
be finite dimensional vector spaces, let
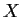
be a
subspace of
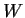
, and let
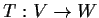
be a linear map. Prove
that the dimension of
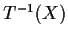
is at least
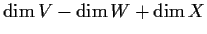
.
Problem 2
Let
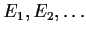
be nonempty closed subsets of a complete metric
space
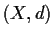
with
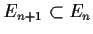
for all positive integers
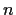
,
and such that
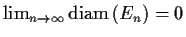
,
where
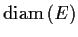
is defined to be
Prove that
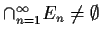
.
Problem 3
Let
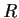
be a ring with
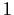
. Suppose that
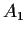
,
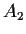
,
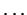
,
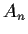
are left ideals in
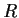
such that
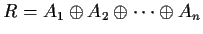
(as additive groups). Prove that there
are elements
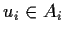
such that for any elements
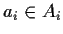
,
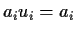
and
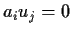
if
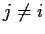
.
Problem 4
Let the rational function
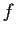
in the complex plane have no poles for
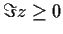
. Prove that
Problem 5
Let
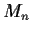
be the vector space of real n
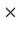
n matrices, identified
in the usual way with the Euclidean space
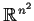
. (Thus, the
norm of a matrix
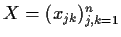
in
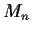
is given by
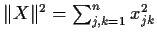
.) Define the map
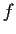
of
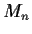
into
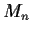
by
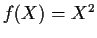
. Determine the derivative
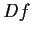
of
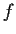
.
Problem 6
Let
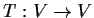
be a linear operator on an
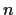
dimensional
vector space
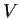
over a field
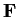
. Prove that
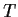
has an
invariant subspace
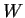
other than
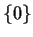
and
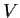
if and only if the
characteristic polynomial of
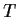
has a factor
![% latex2html id marker 805
$f \in \mbox{\bf {F}}[t]$](img53-54.gif)
with
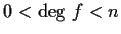
.
Problem 7
Let
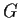
be a finite group acting transitively on a set
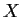
of size at
least
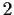
. Prove that some element
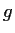
of
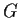
acts without fixed
points.
Problem 8
Evaluate the integral
where the direction of integration is counterclockwise.
Problem 9
Describe all three dimensional vector spaces
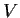
of
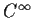
complex valued functions on
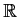
that are invariant under the
operator of differentiation.
Problem 10
Let
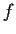
be a continuous real valued function on
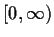
such that
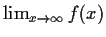
exists (finitely). Prove that
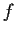
is uniformly continuous.
Problem 11
Let
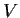
be a finite dimensional vector space over a field
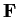
,
and let
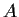
and
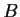
be diagonalizable linear operators on
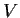
such that
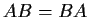
. Prove that
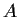
and
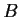
are simultaneously diagonalizable,
in other words, that there is a basis for
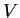
consisting of
eigenvectors of both
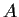
and
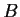
.
Problem 12
Let
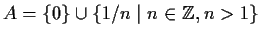
, and let
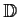
be the
open unit disc in the complex plane. Prove that every bounded
holomorphic function on
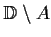
extends to a holomorphic
function on
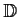
.
Problem 13
Let
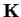
be the field
![% latex2html id marker 971
$\mbox{$\mathbb{Q}\,^{}$}(\sqrt[10]{2})$](img84-50.gif)
. Prove that
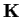
has
degree
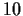
over
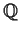
, and that the group of automorphisms of
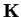
has order
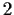
.
Problem 14
Show that every infinite closed subset of
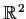
is the closure
of a countable set.
Problem 15
Let
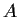
be an n
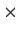
n complex matrix such that
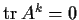
for
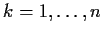
. Prove that
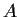
is nilpotent.
Problem 16
For
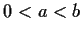
, evaluate the integral
Problem 17
Show that a group
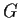
is isomorphic to a subgroup of the additive group
of the rationals if and only if
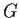
is countable and every finite
subset of
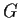
is contained in an infinite cyclic subgroup of
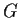
.
Problem 18
Let
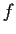
and
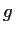
be continuous real valued functions on
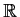
such
that
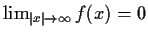
and
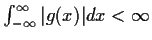
. Define the function
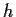
on
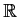
by
Prove that
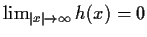
.



Previous: Spring99
Next: Spring00
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10