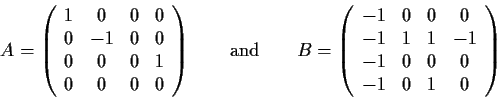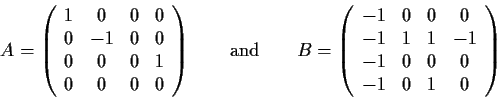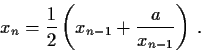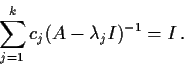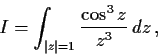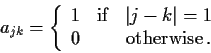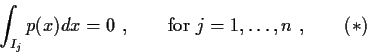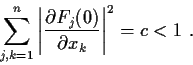Previous: Fall99
Next: Contents
Preliminary Exam - Spring 2000
Problem 1
Are the 4
4 matrices
similar? Explain your reasoning.
Problem 2
Let
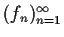
be a uniformly bounded equicontinuous sequence
of real-valued functions on the compact metric space
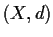
.
Define the functions
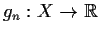
, for
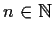
by
Prove that the sequence
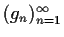
converges uniformly.
Problem 3
Prove that the group
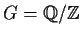
has no proper
subgroup of finite index.
Problem 4
Let
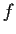
and
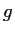
be entire functions such that
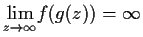
.
Prove that
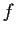
and
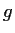
are polynomials.
Problem 5
Let
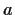
and
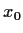
be positive numbers, and define the sequence
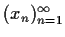
recursively by
Prove that this sequence converges, and find its limit.
Problem 7
Let
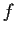
be a positive function of class
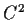
on
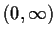
such that
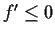
and
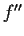
is bounded. Prove that
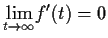
.
Problem 8
Find the cardinality of the set of all subrings of
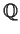
,
the field of rational numbers.
Problem 9
Evaluate
where the direction of integration is counterclockwise.
Problem 10
Let
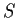
be an uncountable subset of
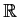
. Prove that there exists
a real number
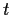
such that both sets
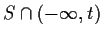
and
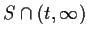
are uncountable.
Problem 11
Let
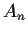
be the
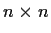
matrix whose entries
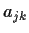
are given by
Prove that the eigenvalues of
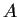
are symmetric with respect
to the origin.
Problem 12
Suppose that
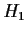
and
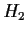
are distinct subgroups of a group
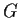
such that
![$[G:H_1]=[G:H_2]=3$](img56-55.gif)
. What are the possible values of
![$[G:H_1\cap H_2]$](img57-55.gif)
? Explain.
Problem 13
Let
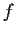
be a nonconstant entire function whose values on the
real axis are real and nonnegative. Prove that all real zeros of
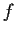
have even order.
Problem 14
Let
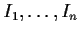
be disjoint closed nonempty subintervals of
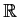
.
- Prove that if
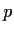 is a real polynomial of degree less than
is a real polynomial of degree less than 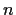 such that
such that
then 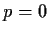 .
.
- Prove that there is a nonzero real polynomial
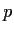 of
degree
of
degree 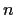 that satisfies
that satisfies 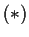 .
.
Problem 15
Let
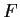
, with components
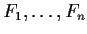
, be a differentiable map
of
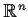
into
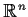
such that
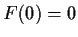
. Assume that
Prove that there is a ball
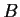
in
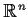
with center
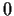
such that
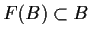
.
Problem 16
Let
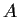
be a complex
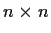
matrix such that the sequence
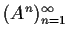
converges to a matrix
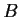
. Prove that
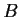
is similar to a diagonal matrix with zeros and ones along the main diagonal.
Problem 17
Evaluate the integrals
Problem 18
Let
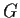
be a finite group and
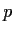
a prime number. Suppose
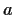
and
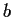
are elements of
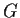
of order
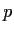
such that
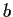
is not in the
subgroup generated by
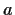
. Prove that
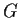
contains at least
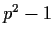
elements of order
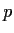
.



Previous: Fall99
Next: Contents
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10