این صفحه شامل چند تصویر است. تا تکمیل آن، کمی صبر کنید.
جلسه ی ششم
موضوع: تساوی دو تابع
توضیح:
در میان نکات زیر، گاهی از شما خواسته می شود فعالیتی را انجام دهید، مطلبی را تعریف کنید یا به سوالی جواب دهید. سعی کنید جواب را در متن کتاب بیابید. اگر در متن کتاب جواب سوال صراحتاً بیان نشده بود، سعی کنید خودتان به سوال مطرح شده پاسخ دهید و اگر نتوانستید از معلمتان بپرسید.
نکات اصلی:
-
به استدلال زیر دقت کنید:
(x+1)}{(x-1)}=\frac{\not{(x-1)}(x+1)}{\not{(x-1)}}=x+1)
آیا این استدلال درست است؟!
سوال:
آیا می توان به دلخواه، هر عدد یا هر عبارتی را از طرفین یک معادله یا از صورت و مخرج یک کسر ساده کرد؟! اگر جواب شما
آری است، به دو استدلال زیر توجه کنید:
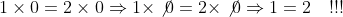
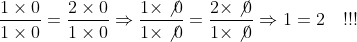
یا استدلال دیگر:
&space;&=&space;-1(x-1)\\&space;x&space;&=&space;-1&space;\end{align*})
و لذا ۱=۱- !!! (کتاب کار ریاضی ۲ جلد اول - وزارت آموزش و پرورش صفحه ی ۶۶)
بنابر این تا مطمئن نشده ایم که
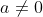
نمی توان از
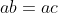
نتیجه گرفت که
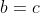
یا این که
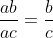
(دقت کنید).
با توجه به نکات بالا، دو تابع
=x+1)
و
=\frac{x^2-1}{x-1})
با یک دیگر برابر نیستند زیرا عدد ۱ در دامنه ی اولی است اما در دامنه ی دومی نیست. بنابر این
اگر دامنه های دو تابع با هم برابر نباشند، آن دو تابع با هم برابر نیستند.
- به استدلال زیر دقت کنید:
برای هر  داریم:
داریم:
}=\sqrt{cos^2(x)}=cos(x))
بنابر این
}&space;&=&space;cos(\frac{2\pi}{3})\\&space;\sqrt{1-sin^2(\frac{\pi}{3})}&space;&=&space;-cos(\frac{\pi}{3})\\&space;\frac{\sqrt{3}}{2}&=&space;-\frac{\sqrt{3}}{2}&space;\end{align*})
که تساوی نادرستی است. پس اشکال استدلال بالا چیست؟ با کمی دقت می توان استدلال بالا را به صورت زیر تصحیح کرد:
}=\sqrt{cos^2(x)}=|cos(x)|)
دو تابع =\sqrt{1-sin^2(x)}) و
و =cos(x)) دارای دامنه های برابر هستند (دامنه ی هر دو
دارای دامنه های برابر هستند (دامنه ی هر دو  است، چرا؟) اما برای بعضی از
است، چرا؟) اما برای بعضی از  های دامنه،
های دامنه، \neq&space;g(x)) ؛ بنابر این
؛ بنابر این
اگر دو تابع f و g دارای دامنه های برابر باشند اما تساوی =g(x)}) برای هر
برای هر  برقرار نباشد، آن گاه دو تابع برابر نیستند.
برقرار نباشد، آن گاه دو تابع برابر نیستند.
- با توجه به نکات ۱ و ۲ می توان مطلب زیر را ثابت کرد:
دو تابع و وقتی و فقط وقتی با هم برابرند که
- اولاً 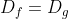 (تساوی دامنه ای)
(تساوی دامنه ای)
- ثانیاً برای هر از دامنه، =g(x)) (تساوی نقطه به نقطه)
(تساوی نقطه به نقطه)
چند مثال:
- دوتابع زیر برابر نیستند، چرا؟
=\sqrt{x^2-1},\,\,\,\,g(x)=\sqrt{x-1}\sqrt{x+1})
(دامنه ها را مقایسه کنید.)
- دو تابع زیر برابرند، چرا؟
=\sqrt{x^2},\,\,\,\,g(x)=|x|)
- دوتابع زیر برابر نیستند، چرا؟
=\sqrt{\frac{x-1}{x+1}},\,\,\,\,g(x)=\frac{\sqrt{x-1}}{\sqrt{x+1}})
- دو تابع زیر برابرند، چرا؟
=cos(k\pi),\,\,g(k)=(-1)^{k}\,\,\,\,\,(k\in&space;\mathbb{Z}))
- دوتابع زیر برابر نیستند، چرا؟
=\frac{x+1}{\frac{1}{x}},\,\,g(x)=x(x+1))
- دوتابع زیر برابرند، چرا؟ (دقت کنید که در این مثال،
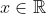 .)
.)
=[x]+[-x],\,\,\,\,g(x)=\begin{cases}&space;0&&space;\text{&space;}&space;x\in&space;\mathbb{Z}&space;\\&space;-1&&space;\text{&space;}&space;x\notin&space;\mathbb{Z}&space;\end{cases})
مساله:
اگر =x-4) و
و =\begin{cases}&space;\frac{x^2-16}{x+4}&space;&&space;\text{&space;}&space;x\neq&space;-4&space;\\&space;k&&space;\text{&space;}&space;x=&space;-4&space;\end{cases}) ،
،  را طوری تعیین کنید که به ازای هر
را طوری تعیین کنید که به ازای هر  ،
، =g(x)) .
.
حل:
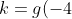=f(-4)=-8)
۲ تیر ۱۳۸۸
آخرین ویرایش صفحه: 6 تیر 1389
نظرات و پیشنهادات شما درباره ی مطالب این صفحه، راه گشای ما است. ما را
از
آن محروم مفرمایید.
با تشکر
6 تیر 1389



