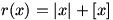این صفحه شامل چند تصویر است. تا تکمیل آن، کمی صبر کنید.
جلسه ی پنجم
موضوع: برد توابع حقیقی
توضیح:
در میان نکات زیر، گاهی از شما خواسته می شود فعالیتی را انجام دهید، مطلبی را تعریف کنید یا به سوالی جواب دهید. سعی کنید جواب را در متن کتاب بیابید. اگر در متن کتاب جواب سوال صراحتاً بیان نشده بود، سعی کنید خودتان به سوال مطرح شده پاسخ دهید و اگر نتوانستید از معلمتان بپرسید.
تعریف برد و توضیحات مهم در این زمینه:
اگر برد تابع حقیقی f به طور صریح داده نشده و تنها ضابطه ی آن در دست باشد، منظور ما از جمله ی «برد تابع f را بیابید»، عبارت است از
«یافتن همه ی خروجی های (f(x که در اینجا x عضوی از دامنه ی f است»، به طور دقیق تر برای محاسبه ی برد تابع f باید مجموعه ی را محاسبه کنیم.
را محاسبه کنیم.
این تعریف نیز همانند تعریف دامنه، بسیار کلی است و قانونی همیشگی برای محاسبه ی برد همه ی توابع وجود ندارد. معمولاً یافتن برد یک تابع، حتی از محاسبه ی دامنه ی آن نیز مشکلتر است و گاهی احتیاج به محاسبات طولانی و نیز داشتن تجربه ی کافی در استفاده از قضایا و فرمولهای ریاضی دارد. ما فقط به چند مثال کلی بسنده می کنیم.
نکات اصلی:
برد توابع چند جمله ای درجه ی 2:
برای یافتن برد تابع =ax^2+bx+c) (که x عددی حقیقی و a عددی مخالف صفر است)، کافی است عرض راس سهمی را به دست بیاوریم.می توان ثابت کرد که این عدد برابر است با
(که x عددی حقیقی و a عددی مخالف صفر است)، کافی است عرض راس سهمی را به دست بیاوریم.می توان ثابت کرد که این عدد برابر است با  (ثابت کنید). اگر
(ثابت کنید). اگر  آنگاه
آنگاه  و اگر
و اگر  آنگاه
آنگاه  . به تصاویر زیر توجه کنید:
. به تصاویر زیر توجه کنید:

به طور مثال برد تابع  برابر است با
برابر است با  زیرا با توجه به نکات بالا
زیرا با توجه به نکات بالا  .
.
-
توابع چند جمله ای درجه ی فرد:
اگر دامنه ی توابع چند جمله ای درجه ی فرد را
R در نظر بگیریم (نه دامنه ای محدود)، آنگاه می توان ثابت کرد که برد نیز R است. (در واقع علت اصلی آن پیوستگی این توابع است که بعدها در دوره ی پیش دانشگاهی به وسیله ی قضیه ی مقدار میانگین اثبات می شود.) به عنوان مثال برد تابع

برابر است با
R .
-
توابعی که می توان به وسیله ی آنها x را بر حسب y محاسبه کرد:
فرض کنید تابع (y=f(x را بتوان به صورت(x=g(y نوشت؛ یعنی
x را بر حسب y محاسبه کرد
. در اینصورت دامنه ی تابع جدید، برد تابع اصلی است. به مثالهای زیر توجه کنید:
الف) برای یافتن برد تابع f با ضابطه ی
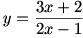
اعمال زیر را انجام می دهیم:
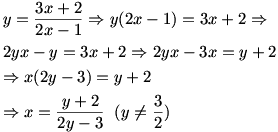
بنابر این
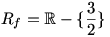
.
به شکل این تابع توجه و سعی کنید برد را فقط به وسیله ی شکل به دست آورید :

نکته: با همین روش ثابت کنید که اگر
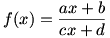
، آنگاه
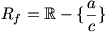
.
ب) برد تابع
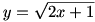
ابتدا توجه کنید که
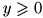
. (دقت کنید که اگر قرار دهیم
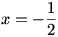
، آنگاه y=0.) می توان نوشت:
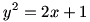
. در نتیجه
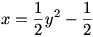
. چون دامنه ی تابع
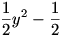
برابر است با
R و چون
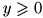
، بنابر این برد تابع
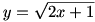
با
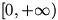
برابر خواهد بود.
به شکل این تابع توجه و سعی کنید برد را فقط به وسیله ی شکل به دست آورید :

ج) برد تابع
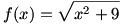
باتوجه به این نکته که طرفین مثبت هستند، می توان نوشت:
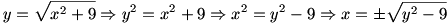
در عبارت آخر، زیر رادیکال باید نامنفی باشد و لذا
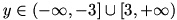
. اما y>0 ، در نتیجه برد تابع f برابر است با
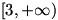
.
به شکل این تابع توجه و سعی کنید برد را فقط به وسیله ی شکل به دست آورید :

د) برد تابع
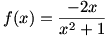 روش اول:
روش اول:
به عبارت زیر توجه کنید:
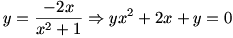
عبارت سمت راست یک معادله درجه ی 2 بر حسب x است. حال با توجه به دلتای این معادله، برای اینکه این معادله جواب داشته باشد باید
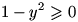
و لذا
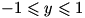
؛ در نتیجه خواهیم داشت:
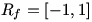
. (توجه کنید که اگر x=-1 آنگاه y=1 و اگر x=1 آنگاه y=-1.)
روش دوم:
با استفاده از اتحاد مربع دوجمله ای، می توان ثابت کرد که
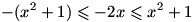
بنابر این
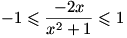
و لذا
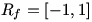
.
به شکل این تابع توجه و سعی کنید برد را فقط به وسیله ی شکل به دست آورید :

ه) برد تابع
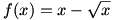
می توان نوشت:
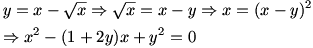
عبارت آخر یک معادله درجه ی 2 بر حسب x است. حال با توجه به دلتای این معادله، برای اینکه این معادله جواب داشته باشد باید
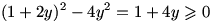
. بنابراین خواهیم داشت:
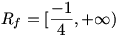
. (روش دیگر برای پیدا کردن برد این تابع، استفاده از مشتق است که به آن نمی پردازیم.)
به شکل این تابع توجه و سعی کنید برد را فقط به وسیله ی شکل به دست آورید :

نکته: مطلب بالا نشان می دهد که کمترین مقدار خروجی این تابع برابر است با
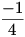
. توجه کنید که اگر
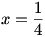
، آنگاه
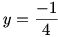
.
-
توابع مثلثاتی:
برد توابع
(sin(x و
(cos(x برابر است با

و برد توابع
(tan(x و
(cot(x برابر است با
R. (چرا؟)
به مثالهای زیر توجه کنید:
الف) برد تابع
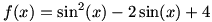
می توان نوشت:
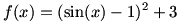
. چون
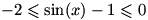
بنابر این
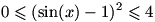
و در نتیجه برای هر

خواهیم داشت
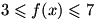
، پس
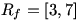
.
ب) برد تابع
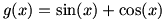
در بخشهای بعدی حسابان خواهید دید که
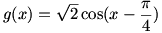
. اما بنابر نکته ی 4 می توان نوشت:
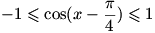
، در نتیجه
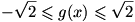
، پس
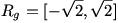
. (توجه کنید که در این مثال و بعضی مثالهای بالا، به طور مخفیانه از قضیه ی مقدار میانگین استفاده شده است که این قضیه را در پیش دانشگاهی خواهید دید.)
نکته ی مهم: ممکن است بعضی از دانش آموزان اینگونه استدلال کنند که چون
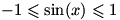
و
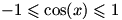
، بنابر این
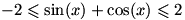
و در نتیجه
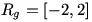
.
این استدلال درست نیست، زیرا برای هیچ x ی
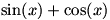
برابر با 2 یا 2- نیست و لذا
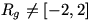
(دقت کنید)! در واقع به وسیله ی استدلال بالا فقط می توان نتیجه گرفت که
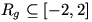
. همین ریزه کاریهاست که محاسبه ی برد بعضی از توابع را مشکل می کند.
به شکل این تابع توجه و سعی کنید برد را فقط به وسیله ی شکل به دست آورید :

-
تابع جزءصحیح:
برد تابع جزءصحیح برابراست با
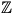
. در حالت کلی برد تابع
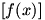
زیر مجموعه ای از
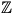
است؛ اما فرمولی کلی برای محاسبه ی برد اینگونه توابع وجود ندارد.
به مثالهای زیر توجه کنید:
الف) برد تابع
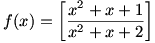
صورت و مخرج کسر
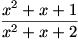
همواره مثبت و صورت کسر از مخرج آن کمتر است. بنابر این
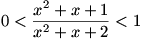
و درنتیجه بنابر خواص جزءصحیح برای هر

، 0=(f(x و لذا باید برد تابع
f مجموعه ی تک عنصری {0} باشد.
ب) برد تابع
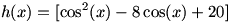
.
می توان دید
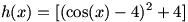
. چون
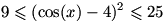
بنابر این
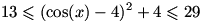
. در نتیجه
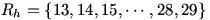
.
ج) برد تابع
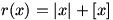
روش محاسبه ی برد این تابع به راحتی به دست نمی آید. برای حدس زدن جواب درست، بد نیست که به شکل متوسل شویم و از آن برای استدلال درست استفاده کنیم. به شکل این تابع توجه کنید:

حال با کمک شکل، می توان جواب را حدس زد و آن را به وسیله ی استدلال استنتاجی اثبات کرد. اگر دوست دارید روش به دست آوردن برد را بدانید،
اینجا را کلیک کنید.
23 شهریور 1386
آخرین ویرایش صفحه: 6 تیر 1389
نظرات و پیشنهادات شما درباره ی مطالب این صفحه، راه گشای ما است. ما را
از
آن محروم مفرمایید.
با تشکر
6 تیر 1389




 را محاسبه کنیم.
را محاسبه کنیم.  (ثابت کنید). اگر
(ثابت کنید). اگر  آنگاه
آنگاه  و اگر
و اگر  آنگاه
آنگاه  . به تصاویر زیر توجه کنید:
. به تصاویر زیر توجه کنید:
 برابر است با
برابر است با  زیرا با توجه به نکات بالا
زیرا با توجه به نکات بالا  .
.  برابر است با R .
برابر است با R .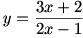 اعمال زیر را انجام می دهیم:
اعمال زیر را انجام می دهیم: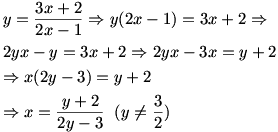
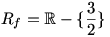 .
.
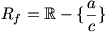 .
.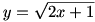
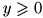 . (دقت کنید که اگر قرار دهیم
. (دقت کنید که اگر قرار دهیم 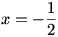 ، آنگاه y=0.) می توان نوشت:
، آنگاه y=0.) می توان نوشت: 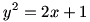 . در نتیجه
. در نتیجه 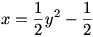 . چون دامنه ی تابع
. چون دامنه ی تابع 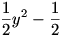 برابر است با R و چون
برابر است با R و چون 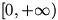 برابر خواهد بود.
برابر خواهد بود.
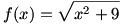
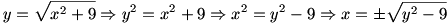
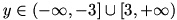 . اما y>0 ، در نتیجه برد تابع f برابر است با
. اما y>0 ، در نتیجه برد تابع f برابر است با 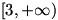 .
.
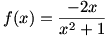
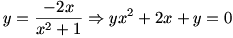
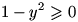 و لذا
و لذا 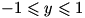 ؛ در نتیجه خواهیم داشت:
؛ در نتیجه خواهیم داشت: 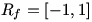 . (توجه کنید که اگر x=-1 آنگاه y=1 و اگر x=1 آنگاه y=-1.)
. (توجه کنید که اگر x=-1 آنگاه y=1 و اگر x=1 آنگاه y=-1.)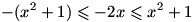
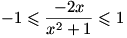 و لذا
و لذا 
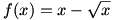
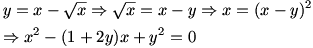
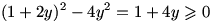 . بنابراین خواهیم داشت:
. بنابراین خواهیم داشت: 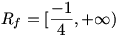 . (روش دیگر برای پیدا کردن برد این تابع، استفاده از مشتق است که به آن نمی پردازیم.)
. (روش دیگر برای پیدا کردن برد این تابع، استفاده از مشتق است که به آن نمی پردازیم.)
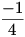 . توجه کنید که اگر
. توجه کنید که اگر 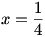 ، آنگاه
، آنگاه 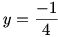 .
. و برد توابع (tan(x و (cot(x برابر است با R. (چرا؟)
و برد توابع (tan(x و (cot(x برابر است با R. (چرا؟)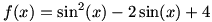
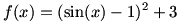 . چون
. چون 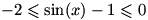 بنابر این
بنابر این 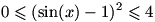 و در نتیجه برای هر
و در نتیجه برای هر  خواهیم داشت
خواهیم داشت 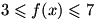 ، پس
، پس 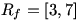 .
.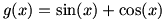
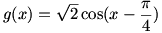 . اما بنابر نکته ی 4 می توان نوشت:
. اما بنابر نکته ی 4 می توان نوشت: 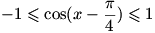 ، در نتیجه
، در نتیجه 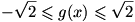 ، پس
، پس 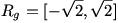 . (توجه کنید که در این مثال و بعضی مثالهای بالا، به طور مخفیانه از قضیه ی مقدار میانگین استفاده شده است که این قضیه را در پیش دانشگاهی خواهید دید.)
. (توجه کنید که در این مثال و بعضی مثالهای بالا، به طور مخفیانه از قضیه ی مقدار میانگین استفاده شده است که این قضیه را در پیش دانشگاهی خواهید دید.)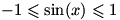 و
و 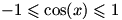 ، بنابر این
، بنابر این 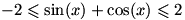 و در نتیجه
و در نتیجه 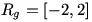 .
. 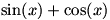 برابر با 2 یا 2- نیست و لذا
برابر با 2 یا 2- نیست و لذا 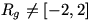 (دقت کنید)! در واقع به وسیله ی استدلال بالا فقط می توان نتیجه گرفت که
(دقت کنید)! در واقع به وسیله ی استدلال بالا فقط می توان نتیجه گرفت که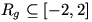 . همین ریزه کاریهاست که محاسبه ی برد بعضی از توابع را مشکل می کند.
. همین ریزه کاریهاست که محاسبه ی برد بعضی از توابع را مشکل می کند.
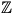 . در حالت کلی برد تابع
. در حالت کلی برد تابع 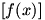 زیر مجموعه ای از
زیر مجموعه ای از 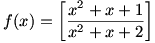
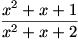 همواره مثبت و صورت کسر از مخرج آن کمتر است. بنابر این
همواره مثبت و صورت کسر از مخرج آن کمتر است. بنابر این 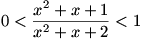 و درنتیجه بنابر خواص جزءصحیح برای هر
و درنتیجه بنابر خواص جزءصحیح برای هر 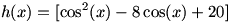 .
.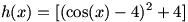 . چون
. چون 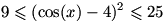 بنابر این
بنابر این 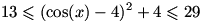 . در نتیجه
. در نتیجه 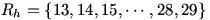 .
.