جلسه ی سوم
تابع و مفاهیم مقدماتی مربوط به آن، ضابطه ی توابع حقیقی
توضیح:
در میان نکات زیر، گاهی از شما خواسته می شود فعالیتی را انجام دهید، مطلبی را تعریف کنید یا به سوالی جواب دهید. سعی کنید جواب را در متن کتاب بیابید. اگر در متن کتاب جواب سوال صراحتاً بیان نشده بود، سعی کنید خودتان به سوال مطرح شده پاسخ دهید و اگر نتوانستید از معلمتان بپرسید.
فهرست مطالب درس
توجه
نکات اصلی
چند مساله همراه با حل
مساله بدون حل
توجه:
دانش آموزان عزیز توجه کنید که مفاهیم فصل اول کتاب (فصل توابع)، برای درک مطالب فصول بعد، بسیار مهم هستند. در واقع مفهوم تابع، اساسی ترین مفهوم حسابان است. برای یادگیری و تسلط بر مفاهیم مربوط به تابع، باید وقت کافی گذاشت و تا حد امکان روی مسائل آن کار کرد.
نکات اصلی:
1. مثالی برای ارائه ی مفهوم تابع: فرض کنید نام ۵ دانش آموز در دفتر نمره ی کلاس با اعداد ۱ تا ۵ مشخص شده باشد. وقتی می نویسیم (۱۷و۲)، یعنی نفر شماره ی ۲ در امتحان ترم اول حسابان نمره ی ۱۷ گرفته است. کدام یک از مجموعه های زیر،روش درستی برای نمایش نمرات حسابان است؟
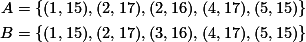
2. در مثال بالا، در مجموعه ی A برای نفر دوم هم نمره 16 و هم نمره ی 17 منظور شده است که چنین چیزی ممکن نیست. در واقع در مجموعه ی A نمره ی نفر دوم مبهم است؛ اما در مجموعه ی B چنین ابهامی وجود ندارد و نمره ی هر کس کاملاً مشخص است.
3. به مجموعه ای از زوجهای مرتب که هیچ ابهامی نداشته باشند (همانند B) یک تابع می گوییم. مجموعه ی A در مثال بالا تابع نیست(چرا؟). به طور دقیقتر:
4. تعریف اول تابع (تعریف کتاب ریاضی 2): تابع مجموعه ای از زوجهای مرتب است که مولفه های اول هیچ دو زوجی با یکدیگر برابر نباشند (و اگر دو زوج با مولفه های اول پیدا کردیم، باید مولفه های دوم نیز برابر باشند. به طور مثال مجموعه ی  یک تابع است.)
یک تابع است.)
5. تعریف دوم تابع (تعریف کتاب حسابان): تابع f از مجموعه ی D به مجموعه ی R قاعده ای است که به هر عنصر x از D به نام دامنه، عنصر منحصر به فرد (f(x از مجموعه ی R به نام هم دامنه را نظیر می کند.
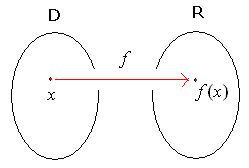
توضیح 1: در تعریف بالا به کلمات قرمز رنگ توجه کنید. در یک تابع باید از
همه ی عناصر دامنه استفاده شود و به هر x از D دقیقاً یک عنصر از R منسوب شده باشد.
توضیح 2: دقت کنید که در یک تابع لازم نیست از همه ی عناصر R استفاده شود.
6. دو تعریف ۴ و ۵ فرقی با یکدیگر ندارند و هر کدام در جای خود مورد استفاده اند.
7. در شکل زیر مشخص کنید از بین 5 رابطه کدام تابع است و کدام تابع نیست و چرا. (یک بار جهت خطوط را از چپ به راست و یک بار از راست به چپ بگیرید.)
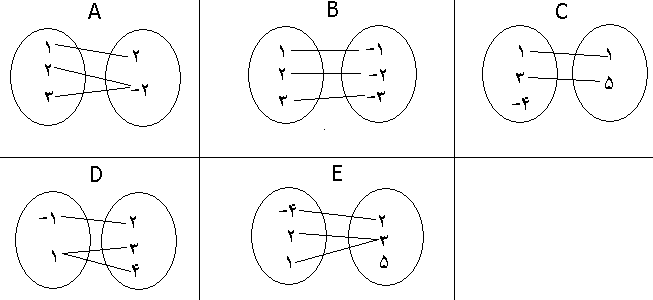
8. تابع را می توان مانند یک ماشین تصور کرد که برای هر ورودی مجاز، یک خروجی منحصر به فرد دارد. (چرا؟)
9. قرار دادها و نمادها: اگر f تابعی با دامنه ی D و هم دامنه ی R باشد می نویسیم:
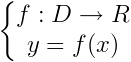 یا
یا 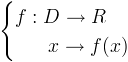
و می خوانیم f تابعی با دامنه ی D و هم دامنه ی R است که هر x از D را به (f(x از R تصویر می کند. (در واقع خروجی x از دستگاه f را (f(x می نامیم.) به  یا
یا  ضابطه یا قانون تابع f گوییم. دامنه ی f را گاهی با
ضابطه یا قانون تابع f گوییم. دامنه ی f را گاهی با  نمایش می دهیم.
نمایش می دهیم.
10. چند مثال:
(الف)  تابعی است که هر عنصر مجموعه ی
تابعی است که هر عنصر مجموعه ی را ابتدا در ۲ ضرب و سپس با ۱ جمع می کند. به طور مثال
را ابتدا در ۲ ضرب و سپس با ۱ جمع می کند. به طور مثال  و
و  ( یعنی تصویر ۰ تحت تابع f عدد ۱ و تصویر عدد 1- تحت تابع f عدد 1- است) و ضابطه ی این تابع
( یعنی تصویر ۰ تحت تابع f عدد ۱ و تصویر عدد 1- تحت تابع f عدد 1- است) و ضابطه ی این تابع  .
.
(ب)  تابعی است که به هر عدد مثبت r، عدد
تابعی است که به هر عدد مثبت r، عدد  را منسوب می کند. به طور خلاصه می توان نوشت:
را منسوب می کند. به طور خلاصه می توان نوشت:  که
که  ؛ یعنی ضابطه ی S با دامنه ی
؛ یعنی ضابطه ی S با دامنه ی  عبارت است از
عبارت است از  .
.
دقت کنید که این تابع مساحت هر دایره را به شعاع آن وابسته می کند و در این مثال مساحت دایره، تابعی است از شعاع آن، یعنی شعاع دایره (یا همان r) متغیری مستقل و مساحت دایره (یا همان S) تابعی از r است. در این حالت به طور خلاصه می نویسیم (S(r. به عنوان مثال اگر شعاع دایره ای 1 واحد باشد، آنگاه (S(1 مساحت این دایره یا همان  است، زیرا
است، زیرا

11. لازم نیست که دامنه یا هم دامنه ی یک تابع، زیر مجموعه ای از اعداد حقیقی باشد. با چنین توابع پیشرفته ای در سالهای بعد آشنا خواهید شد. در حسابان معمولا توابعی را بررسی می کنیم که دامنه و هم دامنه ی آنها زیر مجموعه ای از اعداد حقیقی است.
تابع حقیقی، تابعی است که هم دامنه ی آن زیر مجموعه ای از اعداد حقیقی باشد. برای مشخص کردن یک تابع حقیقی کافی است دامنه و ضابطه ی آن را بدانیم «البته این ضابطه باید چنان باشد که برای هر عضو دامنه یک و تنها یک عنصر از هم دامنه را نظیر کند.»
مثال: دو تابع معرفی شده در نکته ی 10، هردو تابعی حقیقی هستند.
12. اگر یک معادله با دو متغیر به شما داده شده باشد، چگونه می توانید ثابت کنید که این معادله یک تابع را بر حسب یکی از متغیر ها مشخص می کند؟ به طور مثال کدام از معادلات زیر بر حسب x می تواند ضابطه ی یک تابع باشد و کدامیک نمی تواند و چرا؟ (سعی کنید دقیقا توضیح دهید.)

13. (بسیار مهم) برای اینکه نشان دهیم  یک تابع است باید ثابت کنیم از فرض a=b (که a و b عناصری از D هستند)، می توان نتیجه گرفت که (f(a)=f(b (چرا؟).
یک تابع است باید ثابت کنیم از فرض a=b (که a و b عناصری از D هستند)، می توان نتیجه گرفت که (f(a)=f(b (چرا؟).
به طور مثال، ثابت می کنیم که تابع (ب) در نکته ی 10 واقعا یک تابع را نمایش می دهد. به روند منطقی زیر توجه کنید که  :
:

روش دیگری نیز برای اثبات تابع بودن یک رابطه وجود دارد که آن را هنگام حل نمونه مسائل کتاب، توضیح خواهیم داد (به حل تمرین ۴ صفحه ی ۱۸ قسمت (ه) در همین جلسه مراجعه کنید).
14. تابع چند ضابطه ای: بسیاری از توابع را یا نمی توان یا به راحتی نمی توان فقط با یک ضابطه تعریف کرد. توابع مهمی همچون «تابع علامت»، «تابع جزءصحیح»، «تابع دیریکله» و ... از این دست توابع هستند. تابع چند ضابطه ای را به طور دقیق تعریف و حداقل سه مثال از این توابع را ارائه کنید.
چند مساله همراه با حل:
1. عبارت  را برای تابع های زیر پیدا کنید(توجه کنید که در این مساله، h مخالف صفر است):
را برای تابع های زیر پیدا کنید(توجه کنید که در این مساله، h مخالف صفر است):
الف) 
ب) 
حل مساله:
توجه: به روش حل این تمرین دقت کنید و حل آن را کاملا یاد بگیرید. از ایده های به کار رفته در این تمرین، بعدها در فصل مشتق استفاده خواهد شد.
الف)

ب)

2. کدام یک از معادلات (و روابط) زیر در اعداد حقیقی می تواند ضابطه ی یک تابع (بر حسب x) باشد؟
الف) 
ب) 
ج) 
د) 
حل مساله:
الف) فرض کنید x=0. بنابر این y=1 یا y=-1. یعنی اعضای مجموعه ی {(A={(0,1),(0,-1 هر دو عضوی از رابطه ی (الف) هستند. بنابر این رابطه (الف) یک تابع بر حسب x نیست. (بر حسب y چطور؟)
ب) مشابه قسمت (الف) فرض کنید x=0. بنابر این y=0 یا y=2. یعنی (0,0) و (2و0) هر دو عضوی از رابطه ی (ج) هستند. بنابر این رابطه (ج) یک تابع بر حسب x نیست. (بر حسب y چطور؟)
ج) مشابه دو قسمت بالا اگر قرار دهید x=-1، نتیجه خواهد شد: y=-4 یا y=-2. بنابر این رابطه (د) یک تابع بر حسب x نیست. (بر حسب y چطور؟)
د) ثابت می کنیم این رابطه یک تابع بر حسب x است. برای این کار از تعریف اول تابع استفاده می کنیم، به این ترتیب که فرض می کنیم در این رابطه دو زوج مرتب  و
و  صدق می کنند که دارای مولفه های اول مساوی هستند، یعنی
صدق می کنند که دارای مولفه های اول مساوی هستند، یعنی  . ثابت می کنیم مولفه های دوم نیز برابرند؛ یعنی ثابت می کنیم
. ثابت می کنیم مولفه های دوم نیز برابرند؛ یعنی ثابت می کنیم  .
ابتدا توجه کنید که
.
ابتدا توجه کنید که

حال با توجه به توضیحات بالا می توان نوشت:

3. مجموع دو عدد مثبت ۵۰۰ است. اگر یکی از اعداد x باشد تابعی بنویسید، که حاصل ضرب آن دو عدد را به x وابسته کند.
حل مساله:
فرض کنیم x+y=500 و لذا y=500-x. تابع P را حاصل ضرب دو عدد x و y معرفی می کنیم. بنابر این:

4. رابطه ی  را به صورت زوجهای مرتب بنویسید. آیا f یک تابع است؟چرا؟
را به صورت زوجهای مرتب بنویسید. آیا f یک تابع است؟چرا؟
(امتحان نهایی حسابان، ناحیه ی2 زنجان، خرداد 81، بارم: 1 نمره)
حل مساله:
ثابت کنید که {(f={(0,1),(1,0),(0,-1),(-1,0 و لذا f تابع نیست زیرا دارای زوجهایی با مولفه های اول برابر و مولفه های دوم نابرابر است.
5. اگر  یک تابع باشد، مقدار k را محاسبه کنید.
یک تابع باشد، مقدار k را محاسبه کنید.
(امتحان نهایی حسابان، ناحیه ی2 زنجان، خرداد 83، بارم: نیم نمره)
حل مساله:
چون x=2 در هر دو ضابطه ی این تابع هست، بنابر این اگر x=2 را در هر دو ضابطه قرار دهیم باید به یک جواب برسیم (چرا؟) و لذا

27 تیر ماه 1386
مساله بدون حل:
اگر =\frac{x-1}{x+1}) ثابت کنید
ثابت کنید ))\cdot&space;f(x)=-1) .
.
19 آبان 1388
نظرات و پیشنهادات شما درباره ی مطالب این صفحه، راه گشای ما است. ما را
از
آن محروم مفرمایید.
با تشکر
5 تیر 1389





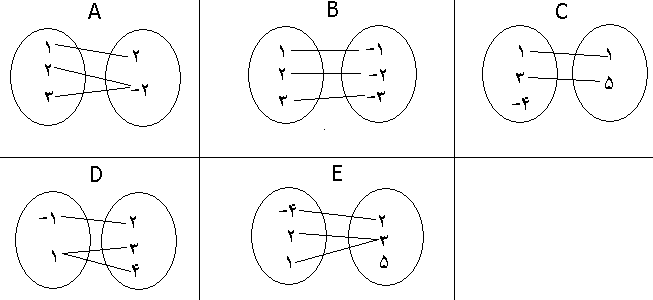
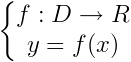 یا
یا 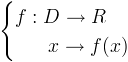
 یا
یا 
 نمایش می دهیم.
نمایش می دهیم. تابعی است که هر عنصر مجموعه ی
تابعی است که هر عنصر مجموعه ی را ابتدا در ۲ ضرب و سپس با ۱ جمع می کند. به طور مثال
را ابتدا در ۲ ضرب و سپس با ۱ جمع می کند. به طور مثال  و
و  ( یعنی تصویر ۰ تحت تابع f عدد ۱ و تصویر عدد 1- تحت تابع f عدد 1- است) و ضابطه ی این تابع
( یعنی تصویر ۰ تحت تابع f عدد ۱ و تصویر عدد 1- تحت تابع f عدد 1- است) و ضابطه ی این تابع  .
. تابعی است که به هر عدد مثبت r، عدد
تابعی است که به هر عدد مثبت r، عدد  را منسوب می کند. به طور خلاصه می توان نوشت:
را منسوب می کند. به طور خلاصه می توان نوشت:  که
که  ؛ یعنی ضابطه ی S با دامنه ی
؛ یعنی ضابطه ی S با دامنه ی  عبارت است از
عبارت است از  است، زیرا
است، زیرا

 یک تابع است باید ثابت کنیم از فرض a=b (که a و b عناصری از D هستند)، می توان نتیجه گرفت که (f(a)=f(b (چرا؟).
یک تابع است باید ثابت کنیم از فرض a=b (که a و b عناصری از D هستند)، می توان نتیجه گرفت که (f(a)=f(b (چرا؟). :
:
 را برای تابع های زیر پیدا کنید(توجه کنید که در این مساله، h مخالف صفر است):
را برای تابع های زیر پیدا کنید(توجه کنید که در این مساله، h مخالف صفر است):







 و
و  صدق می کنند که دارای مولفه های اول مساوی هستند، یعنی
صدق می کنند که دارای مولفه های اول مساوی هستند، یعنی  . ثابت می کنیم مولفه های دوم نیز برابرند؛ یعنی ثابت می کنیم
. ثابت می کنیم مولفه های دوم نیز برابرند؛ یعنی ثابت می کنیم  .
ابتدا توجه کنید که
.
ابتدا توجه کنید که


 را به صورت زوجهای مرتب بنویسید. آیا f یک تابع است؟چرا؟
را به صورت زوجهای مرتب بنویسید. آیا f یک تابع است؟چرا؟ یک تابع باشد، مقدار k را محاسبه کنید.
یک تابع باشد، مقدار k را محاسبه کنید.