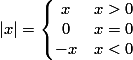پایگاه ریاضیات مقدماتی و تخصصی - آموزش حسابان - اعداد حقیقی - قدر مطلق

این صفحه شامل چند تصویر است. تا تکمیل آن، کمی صبر کنید.

بازگشت به فهرست آموزش حسابان حل و بحث مسائل کتاب حسابان جدید و رفع اشکال

جلسه ی دوم

اعداد حقیقی - قدر مطلق - بازه ها

توضیح:

در میان نکات زیر، گاهی از شما خواسته می شود فعالیتی را انجام دهید، مطلبی را تعریف کنید یا به سوالی جواب دهید. سعی کنید جواب را در متن کتاب بیابید. اگر در متن کتاب جواب سوال صراحتاً بیان نشده بود، سعی کنید خودتان به سوال مطرح شده پاسخ دهید و اگر نتوانستید از معلمتان بپرسید.

فهرست مطالب درس

نکات اصلی

چند مساله همراه با حل

مساله بدون حل

نکات اصلی:

1. اعداد گویا و اعداد گنگ (اصم) را تعریف کنید.

2. معرفی چند عدد گنگ به وسیله بسط اعشاری آنها:

اعداد زیر همگی اعداد گنگ هستند (چرا؟) :

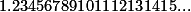
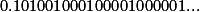
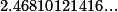
3. به همین ترتیب می توان بی نهایت عدد گنگ ساخت (تنها کافیست بسط اعشاری این عدد، هیچ دوره ی تناوب یا دوره ی تکراری نداشته باشد). بنابر این فقط 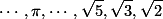  اعداد گنگ نیستند.

4. اعداد 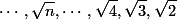را فقط با استفاده از خط کش و پرگار روی خط اعداد حقیقی مشخص کنید. (آیا می توانید به همین وسیله «عدد پی» را روی خط اعداد حقیقی مشخص کنید؟!)

5. تعریف جبری |x| (قدر مطلق x )، که x عددی حقیقی است:

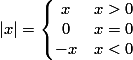
6. تعریف هندسی |x|: قدر مطلق x عبارت است از فاصله عدد x از مبداُ مختصات. به همین دلیل برای هر x داریم: 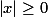 و نیز می توان نوشت: .

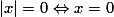7. اگر a و b دو عدد حقیقی باشند، آنگاه |a-b| عبارتست از فاصله ی بین a و b؛ به همین دلیل می توان نوشت: |b-a|=|a-b|

8. فرض کنید a عددی حقیقی و b عددی نامنفی باشد، در اینصورت می توان نوشت:

(الف)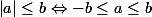

(ب) 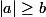 اگر و فقط اگر 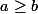یا .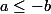

توجه: اگر در (الف) و (ب) همه جا تساویها را برداریم، باز هم عبارات درستی خواهیم داشت.

9. با توجه به نکته ی 6، تعبیر هندسی نکته ی 8 را بیان کنید.

10. بازه های زیر را با استفاده از نماد مجموعه تعریف کنید و آنها را روی خط اعداد حقیقی نمایش دهید(a و b اعداد حقیقی هستند و a از b کوچکتر است):

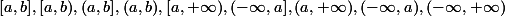
چند مساله همراه با حل:

1. نشان دهید نقطه ی میانی بازه ی (a,b) برابر است با .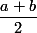

حل مساله:

دو عبارت 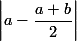 و 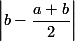 را محاسبه کنید و نشان دهید این دو با یکدیگر برابرند. بنابر نکته ی 7 نتیجه بگیرید که فاصله ی 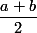از a و b یکسان است.

2. در هر نامساوی، مجوعه ی جواب x را مشخص کنید:

الف)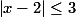

ب)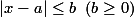

ج)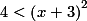

د)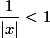

حل مساله:

الف)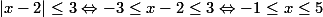

ب) مشابه قسمت (الف) می توان نوشت: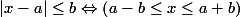

ج) بر اساس نکته ی 7 می توان نوشت:

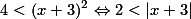
بنابر این 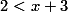یا 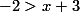. پس مجموعه ی جواب عبارت است از:

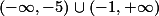
د) برای حل، کافی است نامعادله ی 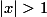را حل کنید.

3. نامعادله روبه رو را حل کنید: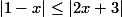

(امتحان نهایی حسابان، ناحیه ی2 زنجان، خرداد 81، بارم: 1 نمره)

حل مساله(روش اول):

بنابر نکته ی7 و نکته ی 8(الف)، می توان نوشت: .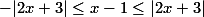

فرض کنید 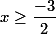. بنابر این 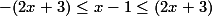. با اشتراک مجموعه جواب هایی که از نامعادلات اخیر به دست می آید، باید داشته باشیم: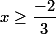

حال فرض کنید 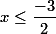. بنابر این 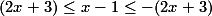. مشابه قسمت بالا، باید داشته باشیم: .

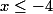بنابر این جواب مساله، مجموعه خواهد بود.

حل مساله(روش دوم):

طرفین معادله را به توان 2 برسانید و پس از ساده کردن، نامعادله ی درجه دوم به دست آمده را حل کنید.

مساله بدون حل:

مساله ی 3 را تعمیم دهید؛ یعنی:
فرض کنید c،b،a و d اعداد حقیقی معلوم باشند. نامعادله ی 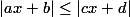را حل کنید.

18 تیر 1386

بازگشت به اول صفحه بازگشت به فهرست آموزش حسابان